¡CAMBIO DE VARIABLE! DIARIO 3

HOLA, BUEN DIA PROFE, LA CLASE PASADA MIRAMOS EL TEMA DE CAMBIO DE VARIABLE SE ME HIZO UN TEMA COMPLEJO, YA QUE TODABIA SE ME COMPLICA UN POCO EN LA RAIZ, PERO SIGO PONIENDO MUCHO DE MI PARTE PARA ENTENDER MEJOR CADA CLASE!



                                          CAMBIO DE VARIABLE

El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.

Para cambiar de variable identificamos una parte de lo que se va a integrar con una nueva variable t, de modo que se obtenga una integral más sencilla.




Pasos para integrar por cambio de variable

1 Se hace el cambio de variable y se diferencia en los dos términos:

 

2Se sutituye la diferencial en la integral:

3 Si la integral resultante es más sencilla, integramos:

4 Se vuelve a la variable inicial:

Ejemplo: Resuelve empleando integración por cambio de variable, la integral

1 Realizamos el cambio de variable

Calculamos la diferencial

2Sustituimos en la integral y simplificamos el integrando

3Resolvemos la nueva integral

4Regresamos a la variable inicial, para ello empleamos 

Así la solución buscada es

Cambios de variables usuales

A continuación enumeramos algunos de los cambios de variables empleados par resolver integrales

1 

2 

3 

4 

5 En las funciones racionales de radicales con distintos índices, de un mismo radicando lineal , el cambio de variable es  elevado al mínimo común múltiplo de los índices.

6 Si  es par:

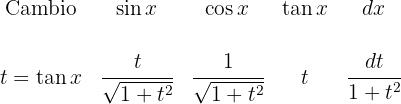
7 Si  no es par:


               referencias

Comments

Post a Comment

Popular posts from this blog

CALCULO DE VOLUMEN PARA SOLIDOS EN REVOLUCION Y METODOS DE ARANDELAS

Image
BUEN DIA PROFE, LA CLASE PASADA MIRAMOS EL CALCULO DE VOLUMEN PARA SOLIDOS EN REVOLUCION Y METODOS DE ARANDELAS EN LO PERSONAL SE ME HIZO UN POCO MENOS COMPLICADO QUE SACAR EL AREA YA QUE PRIMERO ERA SACAR EL RADIO EXTERIOR Y DESPUES RADIO INTERIOR Y DESPUES SE INTEGRA Y EMPESAMOS A RESOLVER EL EJERCICIO ! CALCULO DE VOLUMEN PARA SOLIDOS EN REVOLUCION Y METODOS DE ARANDELAS El cálculo del volumen de sólidos de revolución implica girar una curva alrededor de un eje y luego determinar el volumen del sólido generado. Existen varios métodos para calcular este volumen, siendo los más comunes el método de los discos y el método de las arandelas . 1. Método de los Discos El método de los discos se utiliza cuando la región a girar está directamente adyacente al eje de rotación, sin espacio en el medio. El volumen se calcula sumando volúmenes de discos infinitesimales a lo largo del eje de rotación. 📐 Fórmula: Para una función y = f ( x ) y = f(x) y = f ( x ) girando alrededor del eje ...
Read more

definición de la derivada , 2do parcial diario 1 .

Image
HOLA BUEN DÍA PROFE, LA PASADA CLASE MIRAMOS LA DEFINICIÓN DE LA DERIVADA, SE ME HIZO UN POCO CÓMPLICADO YA QUE ESTOY APRENDIENDO POCO A POCO CON LOS TEOREMAS DE LOS LÍMITES, PERO CON EL BINOMIO ES LO QUE SE ME HIZO POQUITO COMPLICADO PERO ESTAMOS CON TODA LA ACTITUD DE SEGUIR APENDÍENDO .                                                DEFINICIÓN DE LA DERIVADA ¿Qué es la derivada de una función? La derivada de una función matemática es la razón o velocidad de cambio de una función en un determinado punto cuando su variable independiente cambia. Es decir, qué tan rápido se está produciendo una variación. Un sencillo ejemplo es el siguiente. Imagina que hay una función que calcula la posición de un coche en el tiempo. La derivada de esta función, nos indicará a qué velocidad va el coche en cada momento. Derivada de una función: Explicación sencilla Desde una perspecti...
Read more

sustitución trigonométrica 4 parcial

Image
HOLA, BUEN DIA PROFE LA CLASE PASADA VIMOS EL TEMA DE SUSTITUCION TRIGONOMETRICA LA VD SE ME HIZO UN TEMA UN POCO LARGO DE PROCESO Y UN POCO LABORIOSO, PERO ME PONDRE A MIRAR VIDEOS PARA ENTENDERLE UN POCO AL TEMA.         SUSTITUCION TRIGONOMETRICA Sustitución Trigonométrica: Ejemplo Paso a Paso Vamos a resolver la siguiente integral utilizando sustitución trigonométrica : ∫ d x x 2 + 9 \int \frac{dx}{\sqrt{x^2 + 9}} ∫ x 2 + 9 ​ d x ​ 🔍 Paso 1: Identificar el tipo de sustitución Tenemos una raíz del tipo: x 2 + a 2 \sqrt{x^2 + a^2} x 2 + a 2 ​ La sustitución adecuada para este tipo es: x = a tan ⁡ ( θ ) ⇒ d x = a sec ⁡ 2 ( θ ) d θ y x 2 + a 2 = a sec ⁡ ( θ ) x = a \tan(\theta) \quad \Rightarrow \quad dx = a \sec^2(\theta) d\theta \quad \text{y} \quad \sqrt{x^2 + a^2} = a \sec(\theta) x = a tan ( θ ) ⇒ d x = a sec 2 ( θ ) d θ y x 2 + a 2 ​ = a sec ( θ ) En este caso, a = 3 a = 3 a = 3 , entonces: x = 3 tan ⁡ ( θ ) , d x = 3 sec ⁡ 2 ( θ )   d θ x = 3 \tan(\t...
Read more